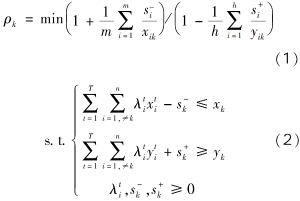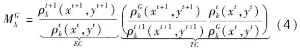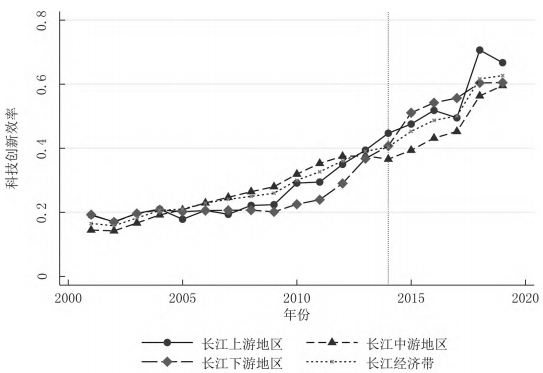
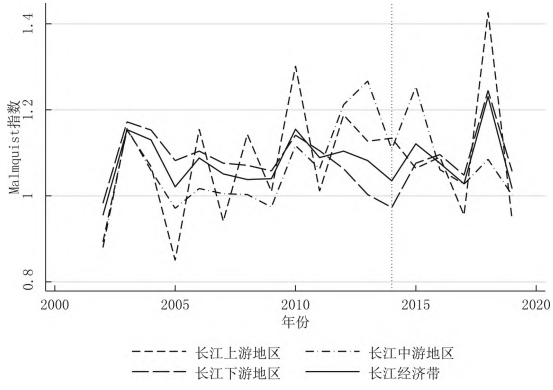
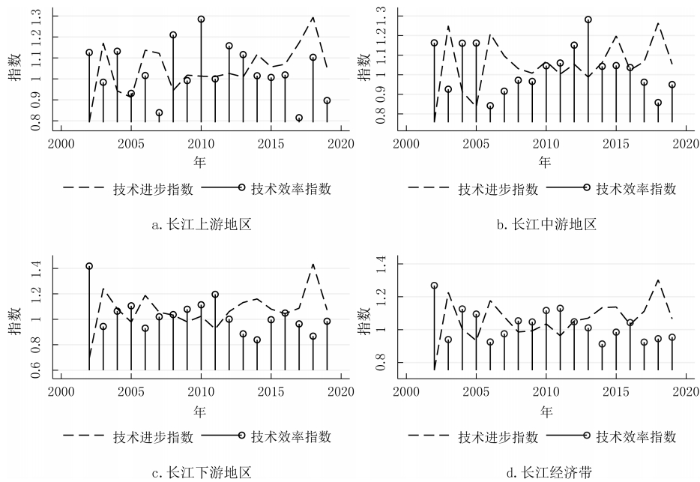
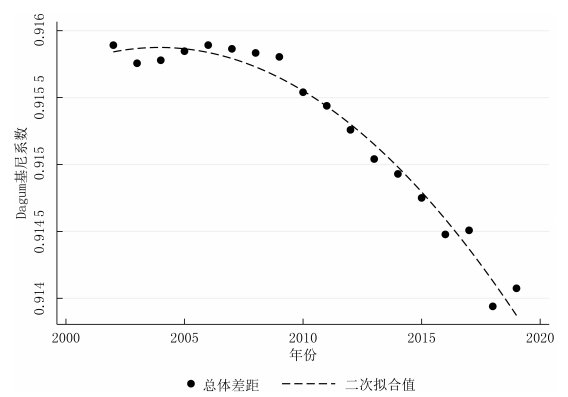
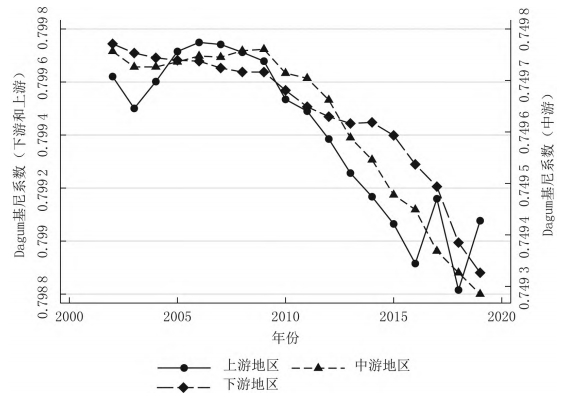
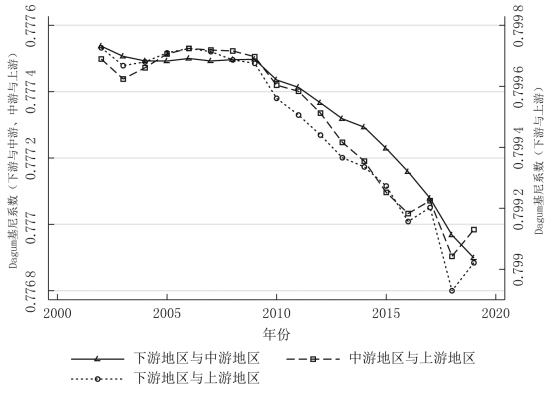
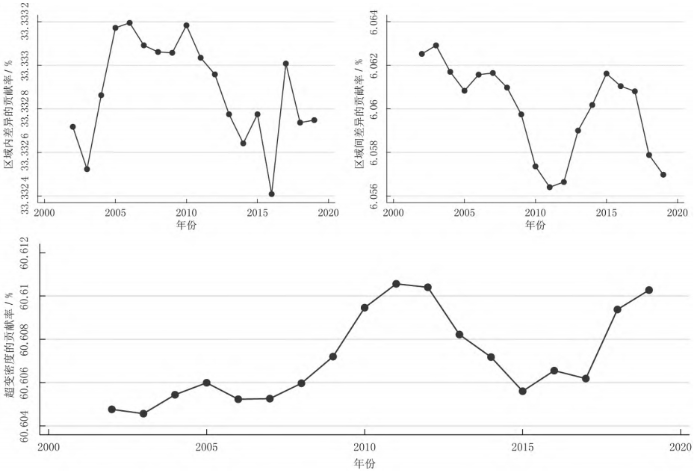
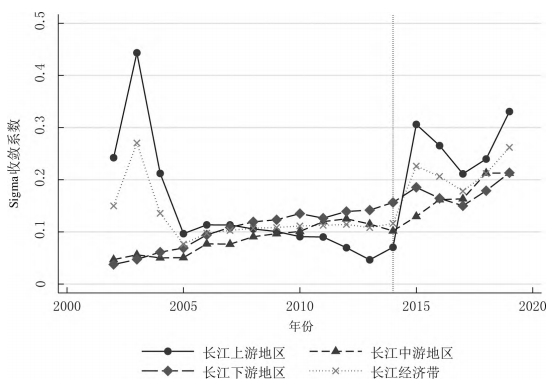
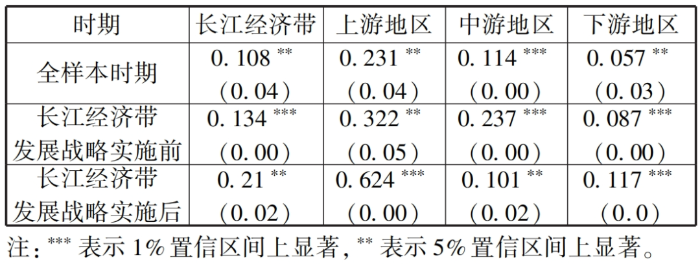
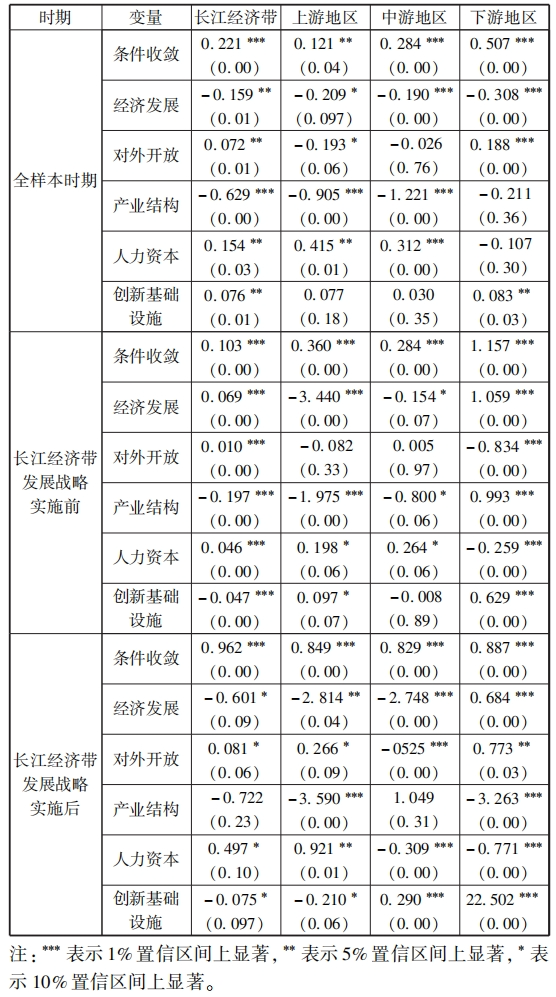
科技创新是长江经济带建设现代经济体系、实现高质量发展的战略支撑，是推动中国式现代化的第一力量。经过多年的对外开放，长江经济带已经融入了全球分工体系，但是大量本土企业被锁定在产业链或者产品价值链的中低端，必须依靠科技创新才能实现在全球价值链上的攀升。同时，虽然长江经济带是我国重要的现代工业集聚地，工业基础扎实、规模庞大，但是关键核心技术仍然缺乏，尤其是在以美国为首的西方国家对华遏制和挑战的情况下，需要以科技创新来解决“卡脖子”问题，加快实现高水平科技自立自强。此外，为了加快经济增长，长江经济带沿线多个省市推进工业化和城镇化，忽略了人与自然的和谐共生，导致长江沿线部分地区环境污染问题突出，生态功能退化，碳排放持续增加。基于此，无论是贯彻落实习近平总书记“共抓大保护、不搞大开发”的指示精神，还是如期或者率先实现碳达峰碳中和目标，都要求长江经济带沿线省市转变发展模式，走生态优先、绿色低碳发展之路，发挥科技创新在经济绿色转型中的支撑作用。

由于科技创新本质上来讲是一种知识生产过程，所以就存在科技创新成果的产出与科技创新资源和要素的投入比问题，即科技创新效率的高低，这种高低变化分别反映在时间和空间上差距：一是在某一区域内科技创新资源和要素投入的持续增长，并没有带来相应的科技创新产出数量增长或者质量的提升；二是将同样的科技创新资源和要素投入到不同区域，其科技创新产出数量或者质量显著不同。这两个维度分别刻画了区域内与区域间科技创新效率的差别，不仅影响了科技创新资源和要素的配置，而且也影响了科技创新对经济发展的贡献程度，成为区域发展不平衡的底层因素之一，给区域协调发展带来了较大的挑战。除此之外，我国依然是世界上最大的发展中国家，科技创新资源较欧美发达国家而言则相对稀缺，这就需要通过提高科技创新效率来实现科技创新资源的最大化利用。

为了更加充分和有效地利用长江经济带科技创新资源，促进长江经济带经济高质量发展，就必须正视科技创新效率在时间和空间上的演变，科学认识科技创新效率向高水平收敛的机制，因此，不仅要考察长江经济带科技创新效率的动态变化规律，还需要充分考虑科技创新效率的区域不平衡问题，即其上、中、下游地区之间以及各自内部科技创新效率的差距变化。本文首先基于数据包络方法测度了长江经济带及其上、中、下游地区的科技创新效率，分解了导致科技创新效率变化的驱动因素，然后利用dagum基尼系数考察了长江经济带及其上、中、下游地区的科技创新效率的空间差距及其形成来源，接着分别采用Sigma收敛和Bate收敛来检验了长江经济带及其上、中、下游地区的科技创新效率的收敛性，最后给出了相关对策启示。

一、文献综述

多年来，我国一直高度重视科技创新在国民经济发展中的重要作用，将推动科技创新做为党治国理政的核心内容之一。在中国共产党第二十次全国代表大会报告提出“必须坚持科技是第一生产力、人才是第一资源、创新是第一动力”。鉴于此，有学者围绕我国科技创新问题从多个角度展开了研究，取得了一批较高质量的成果。这里针对本文的研究目的，主要对科技创新效率方面的相关研究进行了综述。

从现有研究看，针对科技创新效率的测度方法主要是随机前沿模型（SFA）和数据包络分析（DEA）。由于SFA 模型属于参数方式，所以在使用它测度科技创新效率时不仅要事先明确投入变量与产出变量之间的函数关系，而且对变量的平稳性和变量之间的协整关系要求较高。DEA方法采用线性规划技术测算效率，除了不需要事先确定生产函数的形式，还能够完成多投入多产出情形下的科技效率测度，实现不同样本点与效率最优点之间的比较，因此被广泛地采用。譬如，刘爱芹等[1] 、孙凯[2] 、李婧等[3] 、李南等[4] 、李政等[5]利用传统的径向DEA模型对不同区域的创新效率进行了测算，但传统径向DEA模型存在松弛变量、跨期比较和有效率决策单元效率比较等诸多问题，影响了效率测度结果的可靠性，从而推动了新拓展的DEA方法在测度科技创新效率上的应用。其中，王春枝等[6]利用非径向超效率DEA模型测度了我国区域创新效率的动态变化；韩兆洲等[7]采用 Bootstrap-DEA方法测度了中国省际创新效率；朱承亮[8]也使用该方法测算了包括中国在内的36个国家的科技创新效率；白俊红等[9]利用全局参比DEA模型分析了 1998-2012年中国各省市区的区域创新效率；赵庆等[10]利用松弛变量模型（Slacks-Based Measure，简称SBM模型）模型测度了2009-2016 年中国省际科技创新效率；赵凯旭等[11]采用超效率DEA模型（Super-Slacks⁃Based Measure，简称 Super-SBM模型） 研究 2000-2015年省域尺度下我国区域创新效率的时空变化。

由于我国区域发展不平衡现象比较突出，一些学者开始在科技创新效率测度的基础上进一步模型对我国30个省份创新效率进行了测算，并分析了东中西部创新效率，东部地区要明显高于中西部地区，尤其是在科研效率上表现更加明显；赵增耀等[13] 利用2000-2012年数据分析了东部地区、东北、中部地区和西部地区的创新效率，发现中国4个地区创新效率差异显著，呈现东部、东北、中部和西部地区依次递减的特征。在区域差距的测算方法上，为了揭示区域差距的来源，Dagum基尼系数逐步成为研究和分析区域发展空间不平衡问题的重要工具[14-15]研究其时空差距。余泳泽等[12]利用三阶段 DEA模型对我国30个省份创新效率进行了测算，并分析了东中西部创新效率，东部地区要明显高于中西部地区，尤其是在科研效率上表现更加明显；赵增耀等[13]利用2000-2012年数据分析了东部地区、东北、中部地区和西部地区的创新效率，发现中国4 个地区创新效率差异显著，呈现东部、东北、中部和西部地区依次递减的特征。在区域差距的测算方法上，为了揭示区域差距的来源，Dagum基尼系数逐步成为研究和分析区域发展空间不平衡问题的重要工具[14-15]。

近年来，有学者在测度科技创新效率和分析科技创新效率时空差距的基础上，还检验了科技创新效率的收敛性。吕岩威等[16]利用SBM-DEA模型对中国省际绿色创新效率进行测度，在分析其时空跃迁特征的同时，进一步考察了绿色创新效率的收敛性；韩兆洲等[17]在测度我国省际创新效率的基础上，分区域考察了创新效率的动态趋势和变化以及其收敛性质；杨蹇等[18]分别测度了京津冀、粤港澳、长三角、长江经济带和黄河流域等区域科技创新效率，并分析了其时空格局及收敛趋势。

综上所述，目前关于区域科技创新效率的研究已经形成一个基本的框架，即“ 测度—时空格局—收敛性”。本研究虽然立足这一框架，但是在已有的研究上进行了两个方面的拓展：一是以长江经济带及其上、中、下游地区的科技创新效率为研究对象，揭示了其变化趋势、时空格局以及收敛性；二是比较了长江经济带发展战略实施前后科技创新效率的变化趋势、时空格局及收敛性的异同。

二、研究方法与数据说明

（一）全局参比的超效率SBM模型

Pastor等[19]提出可以采用全局参比的SBM模型，以解决传统的DEA效率评价方法不能够对不同效率水平进行跨期比较的问题。本文通过构建全局参比的SBM模型来测度长江经济带科技创新效率，以便进一步分析长江经济带科技创新效率的变化特征。

式中，为科技创新效率；为决策单元的线性组合参数；i和k分别代表第i个DMU和k个现有DMU的数量；和表示第k个投入与产出所对应的松弛变量。

（二）全局参比的Malmquist指数

基于全局参比的超效率SBM模型，第k个DMU的科技创新效率从时期t到时期t+1的跨期变动可以用公式（3）来表示：

式中，

记为全局参比下的Malmquist指数，将其减去1可以得到科技创新效率的增长率，从而可以用来衡量科技创新效率的变化。Cooperate等[20]为了识别效率变化的驱动力，将 Malmquist指数分解为技术效率（EC）和技术进步（TC）。Malmquist指数的分解如式（4） 所示，

和

分别表示在当前参比下时期t和时期t+1的投入产出效率值。

（三）科技创新效率的收敛检验方法

通常用于收敛性检验的方法有Sigma收敛、Beta收敛和俱乐部收敛等，其中Beta收敛又分为Beta绝对收敛和Beta条件收敛，被广泛用于分析不同国家或者区域发展水平的增长率趋势。

科技创新效率的Sigma收敛刻画了不同区域科技创新效率偏离整体水平的离差程度，如果离差随着时间变化而缩小，则认为Sigma收敛[21]存在。在对科技创新效率的Sigma收敛性检验中，通常采用科技创新效率对数的标准差来表示，如式（5）所示：科技创新效率的Sigma收敛刻画了不同区域科技创新效率偏离整体水平的离差程度，如果离差随着时间变化而缩小，则认为Sigma收敛[21]存在。在对科技创新效率的Sigma收敛性检验中，通常采用科技创新效率对数的标准差来表示，如式（5）所示：

式中，表示区域i在时期t的科技创新效率；则为其对数值；Ｎ为区域数量。科技创新效率的Beta绝对收敛表示不同区域的科技创新效率都会趋向同一水平。根据Barro等[21]的方法，Beta 绝对收敛检验的计算如式（6）所示：

式中，和分别为区域i在时期t 和时期t+1时的科技创新效率；则表示区域 i在时期t+1时的科技创新效率增长率；α为常数项；β为需要估计参数；为误差项。当β＜０时，不同区域的科技创新效率趋于收敛；当β＜０时，则趋于发散。如果Beta绝对收敛存在，则意味着科技创新效率低的区域要比科技创新效率高的区域在效率增速上更快，这样才能够收敛到某一个均衡点，然而，在实际的分析中，异质性较大的区域在Beta绝对收敛检验中会趋向于不同的均衡点。针对这种情况，Barro[22]提出了Bate条件收敛，Barro等[21]、Sala⁃i⁃Martin[22]、Mankiw等[23]又继续拓展了Bate条件收敛，他们认为Bate条件收敛认为收敛的速度不仅与初始状态有关，还受到其它因素的影响。此外，按照Galor[24]的研究思路，初始条件不同的各区域在科技创新效率上会形成不同的俱乐部，俱乐部内部条件相似的地区在科技创新效率上会出现收敛，这种情形被称为俱乐部收敛。从计算方法上来说，俱乐部收敛与Bate条件收敛相同。长江经济带沿线省市在经济发展、对外开放、人力资本、产业结构、创新基础设施等方面存在着差异，通过借鉴樊华等[25]、马大来等[26]以及杨骞等[27]的研究，将这些影响因素纳入到β绝对收敛模型，形成了Bate条件收敛模型：

在式（7）中，为区域i在时期t的控制变量k（k=1，２，…，ｎ），是第k个控制变量的回归系数。

（四）样本数据说明与处理方法

为了探索长江经济带科技创新效率的变化特征，本文采用的数据样本为长江经济带沿线11省份，时间跨度为2002-2019年。

投入变量的相关说明。科技创新投入主要有R&D人员和R&D资本存量，其中，R&D人员投入以R&D人员全时当量来表示，R&D资本存量以永续盘存法来进行核算[27]，基期为2001 年。由于R&D资本折旧比传统资本更快，在永续盘存法中将R&D资本的折旧率设定为15％[28]。同时，还通过对名义 R&D进行平减来消除价格因素的影响，平减所需的 R&D价格指数等于消费者价格指数和固定资产投资价格指数的加权平均数，权重分别为55％ 、45％ 。R&D人员全时当量和R&D资本存量所需的R&D经费支出都来自历年《中国统计年鉴》。

产出的变量的说明。科技创新产出可以分别从数量、质量和经济效益等3个维度来体现出来。首先，在数量上，分别就发明专利、实用新型专利和外观设计专利按照50％ 、30％ 和20％ 的权重计算专利数量；其次，在质量上，借鉴寇宗来等[29]的方法，将复旦大学产业发展研究中心发布的城市创新力指数按照省际层面进行加总，得到长江经济带11个省份的2001-2016年的创新能力指数，继而采用指数平滑的方法补齐2017年、2018年和2019年的创新力指数；最后，在经济效益上，由于技术市场交易额通过市场机制反映了科技创新的效益转化能力，所以用技术市场交易额来衡量经济效益。发明专利、实用新型专利和外观设计专利等来自历年《中国统计年鉴》，城市创新能力指数来自复旦大学产业发展研究中心的《中国城市和产业创新力报告2017，技术市场交易金额来自历年《中国科技年鉴》。

在Beta条件收敛模型中，控制变量通过以下具体指标来测度：经济发展水平用人均实际GDP的对数来表示，对外开放程度、创新基础设施水平和产业结构变化分别使用进出口总额、通信业务总收入和第三产业产值占名义GDP的比例来表示，人力资本则用专科以上学历人数占6岁及以上人口总数的比例来表示。人均实际GDP、进出口总额、通信业务总收入、第三产业产值、名义GDP和专科以上学历人数占6岁及以上人口总数等数据均来源于国家统计局数据库和历年《中国统计年鉴》。

三、科技创新效率的变化趋势

（一）科技创新效率的测度结果

在使用数据包络模型进行效率评价时，通常会假设规模收益不变（Contant returns to scale，CRS）或者规模收益可变（ variable returns to scale，VRS）。由于每个DMU不仅在规模上存在差别，而且规模报酬可能出现递增或者递减的情况，因此，与VRS假设下测算的效率结果相比，CRS假设下测算的效率结果可能偏低。当这两种假设下所测度的结果不同时，有学者倾向于选择VRS假设下的测度结果[18,20-31] ，因此本文在比较了在CRS和VRS假设下分别测度的长江经济带科技及其上、中、下游地区的创新效率，选择了VRS假设下的结果。

图1刻画了长江经济带及其上、中、下游地区2001-2019年科技创新效率的变化。在近20年来，在多项产业转型政策、科技政策等的共同作用下，长江经济带科技创新效率持续提高，长江经济带科技创新效率在2001年为0.165，2019年为0.627。其中，长江上、中、下游地区的科技创新效率分别从2011年的 0.191、0.193、0.145提高到2019年的0.667、0.605、0.596。在2001-2004年，长江中游地区的科技创新效率要低于长江经济带的科技创新效率，而长江上、下地区的科技创新效率则高于长江经济带的科技创新效率；在2005-2014年，长江中游地区的科技创新效率快速提升，要高于长江经济带的科技创新效率，而长江上、下游地区的科技创新效率则低于长江经济带的科技创新效率；在2014-2019年，长江中游地区的科技创新效率则低于长江经济带的科技创新效率，长江上、下游地区的科技创新效率则高于长江经济带的科技创新效率，且长江上、中、下游地区的科技创新效率之间的差距较之前变大。从长江上、中、下游地区科技创新效率的变化来看，长江下游地区在长江经济带发展战略提出之前虽然科技创新基础条件、人才储备与科技创新的创新环境等方面都比较好，但是其在科技创新的投入也较大，使得其科技创新效率在较长时间内低于长江中游和上游地区，长江经济带发展战略提出之后，长江下游各省市更加重视科技创新落实长江经济带发展战略的作用，科技创新效率得以提升。长江上游地区科技创新基础条件相对较弱，对创新人才和创新资本的投入也相对不足，所以其在长江经济带发展战略提出前的相当长时间科技创新效率也比较低，随着近些年成都、重庆等中心城市高度重视科技创新在落实长江经济带发展战略中的积极作用，不断优化创新创业环境，增强了对科技创新资源和要素的吸引力，科技创新效率也得到相应地提升。长江中游地区虽然创新资源要低于长江下游地区，但是其科技基础扎实，投入相对长江下游地区要少，使得科技创新效率在长江经济带发展战略提出前十年都高于长江上、下游地区，但是长江经济带发展战略提出后，虽然长江中游地区也增加了对创新的投入，但是创新的产出没有相应的增加，使得其科技创新效率较长江上、下游地区要低。

图１ 科技创新效率的变化趋势

（二）科技创新效率的演变趋势及驱动力分解

图2给出了2001-2019年长江经济带及其上、中、下游地区科技创新的Malmquist指数。科技创新效率的 Malmquist指数反映了本期到下期科技创新效率的变化，可以用于对科技创新效率进行动态分析。从整体上来看，长江经济带科技创新效率的Malmquist指数除了2001年外均大于1，说明长江经济带科技创新效率一直在提高。从分流域来看，长江上游地区创新效率变化较长江中、下游地区的科技创新效率变化幅度大，其中，2005年科技创新效率仅为2004年的85％，而2018年的科技创新效率则为2017年的 142.7％ ；长江中、下游地区的科技创新效率除了个别年份之外科技创新效率的Malmquist指数都大于1，即表明其科技创新效率持续提高。

图２ 科技创新效率的Malmquist指数变化趋势

Malmquist指数可以分解为技术进步指数和技术效率指数，其中，前者主要刻画了由于要素质量的提高和科技技术进步所导致的效率变化程度，后者着重反映了诸如要素配置水平和规模经济水平等的变化在技术不变条件下对效率的影响。从图3中可以看到，在长江经济带发展战略实施之前，无论是长江经济带还是长江上、中、下游地区的科技进步指数大于技术效率指数的年份几乎相等，技术进步和技术效率改善的双重作用驱动了长江经济带及其上、中、下游地区的科技创新效率提高。在长江经济带发展战略实施后，长江经济带及其上、中、下游地区的技术进步指数普遍高于技术效率指数，即科技创新效率的提高更多来自于技术进步。

图３ 科技创新效率的技术进步指数与技术效率指数

四、空间差距及其来源分解

考虑到Dagum基尼系数不仅可以刻画区域空间差距，而且能够将其来源分解地区内差距、地区间差距以及超变密度，因此，这里利用Dagum基尼系数来考察长江经济带及其上、中、下游地区的科技创新效率的空间差距和来源，具体的分解计算方法参见Dagum[32]的做法。

（一）科技创新效率的差距及其演变趋势

图4描述了2002-2019年长江经济带科技创新效率的总体差距，可以看到这些年长江经济带科技创新效率变化具有两个特点：一是长江经济带科技创新效率的 Dagum基尼系数均大于0.9，说明长江经济带科技创新效率长期保持着大的差距；二是长江经济带科技创新效率的Dagum基尼系数随着时间的推移持续减小，尤其是长江经济带发展战略实施后，科技创新效率的Dagum基尼系数缩小的速度加快，即科技创新效率的区域不平衡减缓得更快。

图４ 科技创新效率的总体差距

图5刻画了2002-2019年长江经济带上、中、下游地区内科技创新效率的差距。一是长江经济带上游和下游地区内科技创新效率的Dagum基尼系数均大于0.79，中游地区内科技创新效率的Dagum基尼系数大约0.74，表明在这三大区域内科技创新效率差距较大，且中游地区内科技创新效率差距相对要小于上游和下游地区；二是长江经济带上、中、下游地区内科技创新效率的Dagum基尼系数整体上呈现出明显的下降趋势，表明在这三大区域内科技创新效率的差距趋于缩小；三是长江经济带战略实施后长江经济带上、中、下游地区内彼此之间科技创新效率的差距变大，尤其是长江下游地区内的科技创新效率差距要大于长江上游和中游地区。

图５ 区域内科技创新效率的差距

图6刻画了长江经济带上、中、下游地区间科技创新效率的差距，从图中可以发现，一是长江经济带上、中、下游地区间科技创新效率的Dagum基尼系数均大于0.77，这意味着长江经济带上、中、下游地区间的科技创新效率差距较大；二是长江经济带下游与上游间科技创新效率差距最大，从2010年开始长江经济带下游与中游地区之间科技创新效率的差距要大于同期中游与上游地区之间的科技创新效率差距。三是长江经济带发展战略实施后长江经济带中游地区与上游地区之间科技创新效率的差距和上游地区与下游地区之间的科技创新效率之间的差距在变化上趋于一致。

图６ 区域间科技创新效率的差距

（二）科技创新效率空间差距的来源

图7刻画了2002-2019年长江经济带科技创新效率总体差距的来源。从总体来看，区域内差异、区域间差异和超变密度对长江经济带科技创新效率总体差距的贡献分别约为33.33％ 、6.06％和60.61％ ，超变密度对长江经济带科技创新效率总体差距的贡献最大。从具体分解的长江经济带科技创新效率空间差距的来源来看，区域内差异对长江经济带科技创新效率空间差距的贡献先上升，接着开始下降，最后又有所增加；区域间差异对长江经济带科技创新效率空间差距的贡献先是持续下降，然后上升，在长江经济带战略实施之后又开始下降；超变密度对长江经济带科技创新效率空间差距的贡献在2012年之前基本上是增加状态，随后开始下降，在长江经济带战略实施之后再度回升。尽管从趋势变化上来看，区域内差异、区域间差异和超变密度对长江经济带科技创新效率总体差距的贡献有所变化，但是在从数值角度来看，三者对长江经济带科技创新效率总体差距的贡献基本稳定。

图７ 科技创新效率空间差距的来源

五、收敛性检验

（一）Sigma收敛检验

图8刻画了2002-2019年长江经济带及其上、中、下游地区科技创新效率的Sigma收敛系数的变化情况。长江经济带科技创新效率的Sigma收敛系数除了在205年之前出现短暂明显下跌之外基本上处于上升趋势，这表明长江经济带科技创新效率总体趋向发散。长江中游、下游地区科技创新效率的Sigma收敛系数长期呈上升趋势，长江上游地区Sigma收敛系数在2006-2013年之间出现了持续小幅下降之后又开始上升。在长江经济带发展战略实施之后，长江经济带及其上、中、下游地区科技创新效率的Sigma收敛系数上升更加明显。综上所述，长江经济带及其中、下游地区的科技创新效率几乎未呈现出Sigma收敛特征，长江上游地区的科技创新效率则在一段时间内呈现了 Sigma收敛特征。

图８ 科技创新效率的Sigma收敛系数

（二）Beta绝对收敛检验

表1给出了Beta绝对收敛和绝对俱乐部收敛检验结果。从全样本时期看来，长江经济带及其上、中、下游地区的科技创新效率的Beta系数显著为正。因此，长江经济带及其上、中、下游地区的科技创新效率都不存在Beta绝对收敛。从分时期来看，无论是长江经济带发展战略实施前还是后，长江经济带及其上、中、下游地区科技创新效率都不存在Beta绝对收敛，且长江经济带发展战略实施后，除了中游地区外，长江经济带及其上、下游地区的科技创新效率Beta系数明显增加，表明扩散的程度进一步加大。

表１ Beta绝对收敛和绝对俱乐部收敛检验结果

（三）Beta条件收敛检验

长江经济带从上游到下游地区在经济发展水平、科技创新基础条件等方面存在较大差异，Beta绝对收敛的结果可能会受到外部因素的影响而改变，因此，本文进一步考察了Beta相对收敛和条件俱乐部收敛，其检验结果见表2。

无论是从全样本时期来考察，还是分为长江经济带发展战略实施前后来看，长江经济带及其上、中、下游地区都不存在Beta条件收敛，其中，长江经济带发展战略实施后，Beta的值变得更大。事实上，收敛性反映了样本的差异随着时间推移而降低的特性，并最终处于一种均衡状态，但是由于样本所处的发展阶段以及外部条件的影响，样本的差异在某个时段，尤其是处于快速发展时期或者受到外部条件的强力干预，可能不仅没有降低，反而扩大了，即所谓的扩散。无论是从前述的Sigma收敛和Beta绝对收敛，还是这里的Beta条件收敛，长江经济带及其上、中、下游地区的科技创新效率几乎都倾向于扩散，且长江经济带发展战略实施之后扩散程度加剧，主要是因为长江经济带及其上、中、下游地区处于创新发展转型阶段，经济发展水平、科技创新要素与资源等的差异导致科技创新效率的时空差距变化较大，长江经济带发展战略的实施加强了转型力度，扩大了多个区域科技创新效率的差距。

表２ β 相对收敛和条件俱乐部收敛检验结果

从全样本时期控制变量对科技创新效率的影响来看，经济发展降低了长江经济带及其上、中、下游地区的科技创新效率。盛彦文等[33]认为经济发展水平的提高可以为科技创新提供更多的研发资金，从而可以提升科技创新需求与科技创新效率。不过，如果存在规模经济，就会出现经济发展水平提高后更多的资金投入到扩大再生产，创新的成果也可能由于不能够快速规模化而被搁置，这种情形下经济发展水平的提高反而降低了科技创新效率。通过观察长江经济带沿线省市产业的发展情况，虽然涌现了一批创新型企业，但是整体而言，长江经济带沿线省市的经济发展还是依赖规模驱动的。对外开放水平的提高促进了长江经济带及其下游地区科技创新效率的提高，降低了上游地区的科技创新效率，对中游地区科技创新效率的影响不显著，主要是长江下游地区外向型经济比较发达，FDI的技术溢出效应和企业间为了出口而展开竞争共同促进了技术创新效率的提升。相对而言，长江上游地区外向型经济水平不高，为了追求低技术水平产品的出口规模而忽略了科技创新。由于当前科技创新主要出现在工业领域，第三产业比重的提升降低了第二产业的相对规模，可能会减少创新成果。因此，第三产业比重的提高降低了长江经济带及其上、中游地区的科技创新效率。人力资本的提升促进了长江经济带及上游、中游地区的科技创新效率，马大来等[26]认为人力资本素质越高，有利于加快新技术的扩散速率，提升科技创新效率。创新基础设施的改进显著地提高了长江经济带及其下游地区的科技创新效率，创新基础设施是实现科技技术突破、促进科技成果转化、支撑创新创业的重要基础，以“宽带中国”战略以及5G为代表的新基建不仅降低了创新过程中信息传递的成本，而且不断拓展新的创新领域，从而有效地促进科技创新效率的提高。

通过比较长江经济带发展战略实施前后的分时段情况下控制变量对科技创新效率的影响来看，其主要区别如下：一是在长江经济带发展战略实施之前，经济发展促进了长江经济带科技创新效率的提升，而长江经济带发展战略实施之后经济发展则降低了科技创新效率；二是长江经济带发展战略实施后对外开放对科技创新效率的影响显著增强，对外开放促进了长江经济带及其上游、下游地区科技创新效率的提高，降低了中游地区的科技创新效率；三是长江经济带发展战略实施前第三产业比重增加提高了长江下游地区的科技创新效率，但是长江经济带发展战略实施之后则恰恰相反，且对长江经济带及其中游地区的科技创新效率没有显著影响；四是长江经济带发展战略实施后人力资本对科技创新效率的影响增强，且人力资本增加降低了长江中游地区的科技创新效率；五是创新基础设施的提升在长江经济带发展战略实施之前促进了上、下游地区科技创新效率的提高，但是在长江经济发展战略实施后其降低了长江上游地区的科技创新效率，提高了长江中、下游地区的科技创新效率。长江经济带发展战略实施前后这些控制变量对科技创新效率的影响差别可能由于发展战略与发展方式的深刻转变，导致这些控制变量对长江经济带及其上、中、下游地区科技创新效率的影响程度出现了相对变化，譬如，长江经济带发展战略实施后各地更加重视创新发展，由于长江中、下游地区经济发展水平相对较高，其对创新基础设施建设投入更大，创新基础设施的提升对科技创新效率的影响超过了人力资本增加，使得人力资本的提升可能会降低科技创新效率，与此同时，长江上游地区由于经济发展水平的原因导致创新基础设施建设相对不足，人力资本增加对科技创新效率的影响则高于创新基础设施的提升，也使得创新技术设施的提升可能会降低科技创新效率。

六、结论与对策建议

（一）结论

为了探究长江经济带科技创新效率的时空格局与收敛性，首先使用GS-SBM模型测度了长江经济带及其上、中、下游地区的科技创新效率，其次利用Malmquist指数考察了科技创新效率的变化趋势及其驱动力，再次通过Dagum基尼系数考察了长江经济带及其上、中、下游地区的科技创新效率的区域差距，并分析了区域差距的来源，最后，分别采用Digma收敛、Beta绝对收敛和Beta条件收敛方法检验了长江经济带及其上、中、下游地区科技创新效率的收敛性。

一是长江经济带及其上、中、下游地区的科技创新效率呈现持续提升趋势，其中，长江经济带发展战略提出之后，长江经济带及其上、中、下游地区的科技创新效率更加明显，且彼此间的差距有所扩大；二是Malmquist指数的结果进一步验证了长江经济带及其上、中、下游地区的科技创新效率持续提升，同时，Malmquist指数的分解结果表明在长江经济带发展战略实施之前科技创新效率的提高来自技术进步与技术效率的双重驱动，但是在高更多地来自技术进步；三是长江经济带及其上、中、下游地区的科技创新效率一方面存在较大的空间差距，但是另外一方面这种差距也有趋于缩小，超变密度对长江经济带科技创新效率的总体差异贡献最大；四是无论是Sigma收敛法还是Beta绝对（相对）收敛法都说明长江经济带及其上、中、下游地区的科技创新效率处于扩散状态，且长江经济带发展战略的实施强化了这一扩大态势；五是经济发展水平、对外开放程度、产业结构调整、人力资本与创新基础设施的投入都会影响到长江经济带及其上、中、下游地区的科技创新效率，但是由于不同区域的发展水平、发展模式、资源禀赋等方面的差异，这些因素对科技创新效率的影响不同，且在长江经济带发展战略实施之后，也改变了其对科技创新效率的影响程度。

（二）对策建议

第一，科学客观地看待长江经济带科技创新效率的差距。一方面由于长江经济带上、中、下游地区创新的基础条件与资源禀赋存在较大的差异，客观上导致了科技创新效率的区域差异， 另外一方面长江经济带上、中、下游地区科技创新效率的差距是在发展中形成的差距，即长江经济带上、中、下游地区的科技创新效率一直保持着提升的趋势，并非大幅度提升与下降之间形成的差距，且这些差距呈现出下降趋势。习近平总书记指出不平衡是普遍的，要在发展中促进相对平衡。要实现长江经济带及其上、中、下游地区科技创新效率的区域协调，要坚持因地制宜的原则，根据各地区科技创新的基础条件和比较优势，不断优化科技创新要素与资源的配置水平，形成有效的科技创新效率提升路径。

第二，积极发挥长江经济带发展战略对提升科技创新效率的作用。长江经济带发展战略实施后不仅各地区科技创新效率明显提高，而且没有导致科技创新效率的收敛程度缩小，这说明长江经济带发展战略可能加速了科技创新效率的提高。长江经济带发展战略通过构建现代产业体系、建设新型城镇化和区域一体化，深刻地改变了新的集聚效应，改善了科技创新资源与要素的配置效率。因此，要继续深入贯彻习近平总书记关于长江经济带发展战略的指示精神，积极落实《长江经济带发展规划纲要》《“十四五”长江经济带发展实施方案》等战略规划，以长江经济带的高质量发展提升科技创新效率。

第三，大力落实科教兴国战略来增强提升科技创新效率的动力。科技创新效率强调了科技创新资源与要素的节约、高效利用，但是并不否认创新投入与产出的扩大以及创新成果水平的提高，事实上，长江经济带作为国家重大战略发展区域之一，更加需要科技创新成果的量质齐升，由此可见，长江经济带的科技创新效率提高是要建立在统筹科技创新规模与质量的基础之上。要提高科技创新的规模与质量，除了扩大创新资源与要素的投入外，还需要提高这些创新资源与要素的质量，并利用科技创新体制机制的改革来破解制约创新的制度型障碍。通过落实科教兴国战略，能够为科技创新提供高质量的创新资源与要素以及良好的创新环境，为科技创新效率的提升提供源源不断的强大动力。

注：原文载自《中国软科学》2024年第1期。文中部分图片来源于网络，版权归原作者所有。